Beauty in Math: Euler's Irrational Imagining
The poem that follows is a tribute to Euler's magnificent observation that :
What is interesting about the above equation is the fact that it involves 3 of the most important numbers in Math: the imaginary number i , and the irrational numbers e (Euler's number) and pi. Morover, it shows that an imaginary number raised to an imaginary number could actually result in a real number! Contemplating this equation, one could not but appreciate the inherent beauty that exists in math.
Sidelight
I consulted a professor one time. We discussed the graph output of the results of my experiments. After staring at the graph for a couple of seconds, he suddenly smiled and said "It's beautiful, isn't it?" Of course, I could not disagree, lest he gives me a failing mark. So I just parrot him and said "Uhmm..ah...yes... it's beautiful!"
Euler's Irrational Imagining
i to the iyou equal, do you not,one over the square root ofe to the pi?
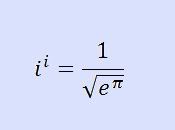





Comments
Post a Comment